
创建回归拟合叠加图层 |

|

|

|
|
|
创建回归拟合叠加图层 |

|

|

|
创建回归拟合叠加图层
|
|
||
为回归定义一个公式固然有用,但有时我们更想把线性拟合用数据点显示出来。在这一节中,我们将使用一个为线性数值创建的线性拟合,然后把它叠加到散点图上。
| 1. | 请导入样本教程数据库中的Linear Regression Analysis(线性回归分析)里的FITC MESF Beads Completed.fey版面。 |
| 2. | 请来到版面上的第2页。 |
| 3. | 请选择Data(数据)→Save/Load(保存/导入)→Custom Data(自定义数据)→New Custom Data(新建自定义数据)命令。 |
| 4. | 请把新建的自定义数据命名为Regression Line Fit(回归线性拟合)(图T27.17)。 |
| 5. | 请把Columns(列)数改为2(图T27.17)。 |
| 6. | 请把Rows(行)数改为10(图T27.17)。 |
| 7. | 请选中Open Data Grid(打开数据网格)复选框(图T27.17)。 |
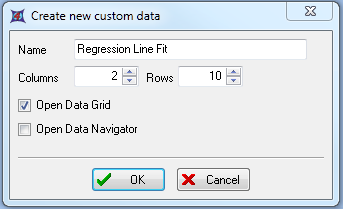
图T27.17 Creating a New Custom Data Grid with 2 Columns and 10 Rows (创建一个有着2列10行的新建自定义数据网格)
| 8. | 请点击OK。 |
我们将使用该自定义数据网格来为线性拟合计算数值,计算的依据是版面中散点图上的公式。我们首先来计算一列X值,计算的根据是后面要通过直线公式用来计算Y值的那些数据。
这一系列X值必须根据你的数据分成数据区间。在这个数据组中,中间数的范围大约从40到5500(自定义数据网格中的Median(中间数)一列)。在本例中,我们把这些值分成10个数据区间,区间之间的步进值是546[(5500-40)/10 = 546]。我们把546四舍五入到600,所以最后的数值范围是40到5440。这里定义的范围将给出直线的上下边界。我们将使用参数数学来计算数据网格中的10行数值。
| 9. | 请点击Regression Line Fit(回归线性拟合)自定义数据网格来将其选中。 |
| 10. | 请选择Data(数据)→Calculate(计算)→Parameter Math(参数数学)→Single Calculation(单个计算)命令。 |
| 11. | 请把Output Parameter(输出参数)修改为A(图T27.18)。 |
| 12. | 请点击Formula(公式)单选按钮(图T27.18)。 |
| 13. | 请输入以下公式:"=40+(Row-1)*600"(图T27.18)。 |
| 14. | 请点击Calculate(计算)(图T27.18)。 |
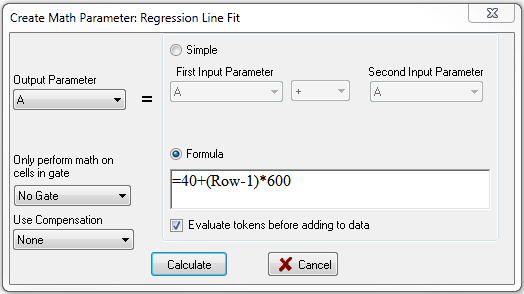
图T27.18 Defining Parameter Math for Column A in the Regression Line Fit Custom Data (为回归线性拟合自定义数据中的A列定义参数数学)
数据网格中的列A将被这些参数数学计算出的数值所填充。我们使用的公式把40设为最小值并使用当前的行号减去一作为每一区间的乘数。计算的结果就是自定义数据网格中的数据表格,如图T27.19所示。
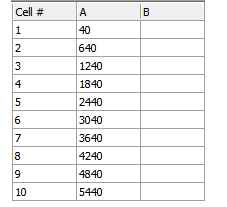
图27.19 Column A Calculated by Parameter Math (由参数数学计算的列A)
我们现在将根据线性拟合来计算Y值,计算将基于自定义标记Linear Fit for Overlays(叠加图层对应的线性拟合)为直线定义的公式,该自定义标记是通过和创建线性回归标记一节中相似的步骤创建的。
| 15. | 请点击Regression Line Fit(回归线性拟合)自定义数据网格来将其选中。 |
| 16. | 请选择Data(数据)→Calculate(计算)→Parameter Math(参数数学)→Single Calculation(单个计算)命令。 |
| 17. | 请把Output Parameter(输出参数)修改为B(图T27.20)。 |
| 18. | 请点击Formula(公式)单选按钮(图T27.20)。 |
| 19. | 请在公式文本框中输入以下文本: =LinearXtoY(P1, [ |
| 20. | 请在公式中的方括号后右键点击。 |
| 21. | 请点击Insert Token(插入标记)。 |
| 22. | 请插入在Custom(自定义)选项下的Linear Fit for Overlays(叠加图层对应的线性拟合)标记。 |
| 23. | 请点击Insert(插入)。 |
| 24. | 请键入一个右侧方括号,然后键入圆括号的右半部,完成标记输入。 |
请取消对Evaluate tokens before adding to data(在将其插入数据前评估标记)复选框的选择(图T27.20)。
最后的公式看起来应该如图T27.20所示。
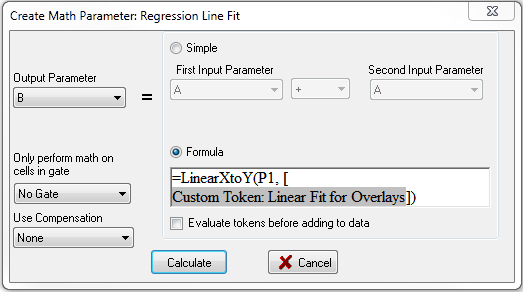
图T27.20 Defining the LinearXtoY Function (定义LinearXtoY函数)
| 25. | 请点击Calculate(计算)。 |
数据网格将进行更新,显示从直线公式以及数据网格中的X值计算出的Y值(LinearXtoY公式中的X值由P1=Parameter 1(参数1)=Column A(A列)定义),如图T27.21所示。
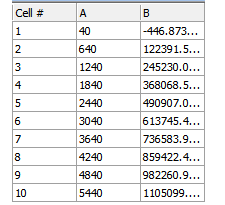
图T27.21 Completed Custom Data Grid for Linear Regression (为线性回归设置好的自定义数据网格)
我们现在将把数据网格叠加到散点图上,以显示直线拟合。
| 26. | 请右键点击散点图。 |
| 27. | 请从弹出菜单上选择Add overlay(添加叠加图层)。 |
| 28. | 请选择Active Files(当前文件)标签(图T27.22)。 |
| 29. | 请在Regression Line Fit(回归线性拟合)上双击(图T27.22)。 |
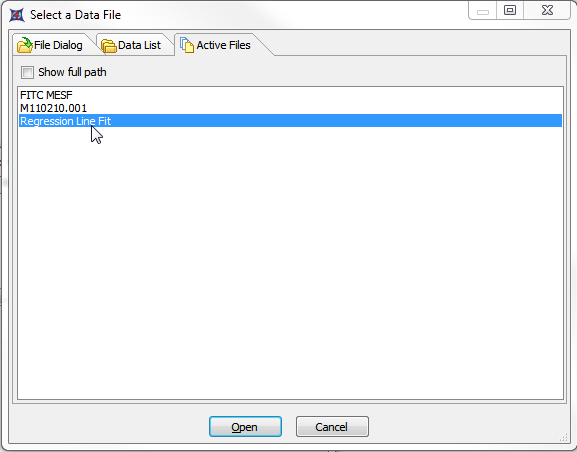
图T27.22 Choosing Regression Line Fit as an Overlay (选中回归线性拟合作为叠加图层)
| 30. | 请在Add overlay(s) for:(添加叠加图层于:)对话框上点击OK。 |
回归直线将以红色数据点出现在散点图上(图T27.23)。我们将对散点图进行格式化,把回归变成一条简单直线。
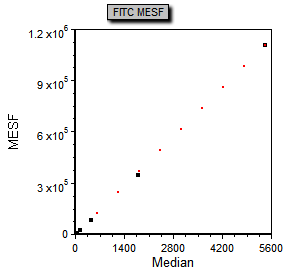
图T27.23 Regression Line Fit Data Overlayed on the Scatter Plot (叠加于散点图上的回归直线拟合数据)
| 31. | 请右键点击散点图。 |
| 32. | 请从弹出菜单上选择Format(格式)。 |
| 33. | 请选择Overlays(叠加图层)类别选项。 |
| 34. | 请选择Regression Line Fit(回归直线拟合)叠加图层。 |
| 35. | 请把Point Shape(数据点形状)修改为Do Not Show(不显示)。 |
| 36. | 请点选Connect the points(连接数据点)复选框。 |
| 37. | 请点击OK。 |
散点图现在看起来应该如图T27.24所示,其中原始数据显示为数据点,而回归直线拟合显示为一条黑线。
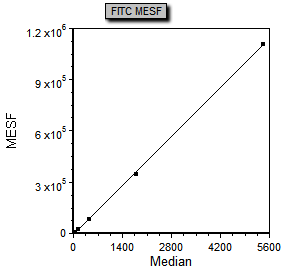
图T27.24 Scatter Plot Displaying Raw Data as Dots and the Regression as a Black Line (把原始数据显示为数据点、把回归数据显示为一条黑线的散点图)
在下一节中,我们将把线性回归应用到一个FCS数据文件上,以获取MESF数据。