Defining a k-means cluster analysis(定义k-means聚类分析)

k-means聚类分析在FCS Express 中通过Transformation(转换)按钮，位于Tools(工具)标签→ Transformations来展示。 下面的步骤概述了在您的数据上创建一个新的k-聚类分析的过程。

 

1.打开Transformation(转换)窗口通过选择Tools(工具)标签→ Transformations→Transformations命令(如下图, Step 1).
2.点击与蓝色加号按钮相邻的greenplus下拉箭头(图下面的步骤2)。
3.点击Kmeans在下拉菜单中(图29.21, Step 3)。

 

(Figure 29.27) - A Kmeans transformation can be created via the Transformations navigator.

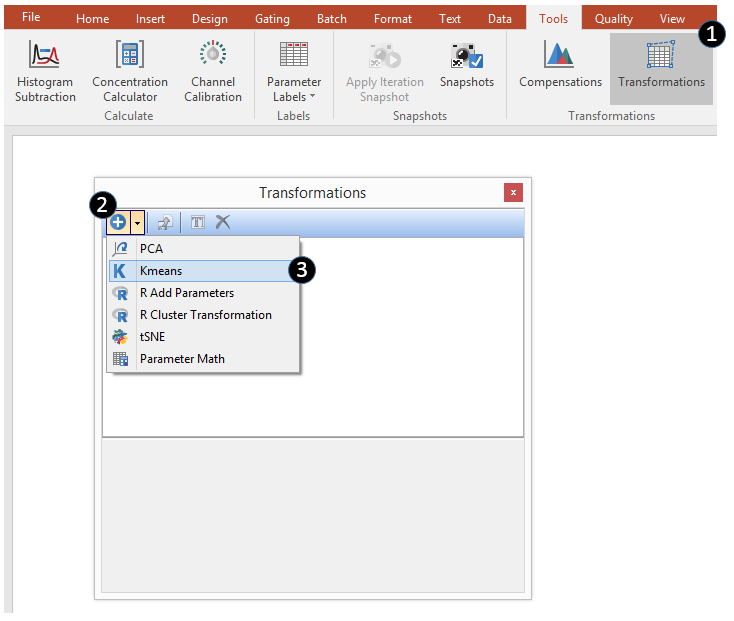
(Figure 29.27) - A Kmeans transformation can be created via the Transformations navigator.

 

此Kmeans对话框现在会出现，在Transformation(转换)窗口中，如图29所示22。

 

Figure 29.28 -The Kmeans dialog opens when a new k-means transformation is created.

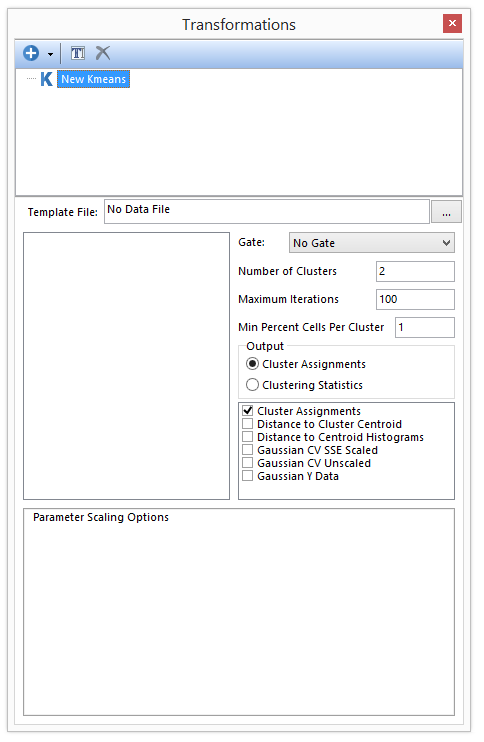
Figure 29.28 -The Kmeans dialog opens when a new k-means transformation is created.

 

这新的Kmeans transformation 被命名为默认的New Kmeans它也能简单的通过如下两种方法重命名:

•在Kmeans transformation 上右击，需要重命名→选择Rename(重命名)。
•选择Kmeans transformation，重命名可以通过左键和按键盘上的F2键。
•选择Kmeans transformation，重命名可以通过左键和点击NewRenameTransformations工具栏的按钮。

 

4.为k-means聚类 选择一个模板文件通过点击Template File编辑框右侧的省略号。

 

  一旦你感兴趣的文件被选择，将使用可用参数的列表填充对话框，以便根据模板文件中的可用参数执行k-means聚类(图2923)。

Figure 29.29 - A template file has been loaded into the New Kmeans dialog. 

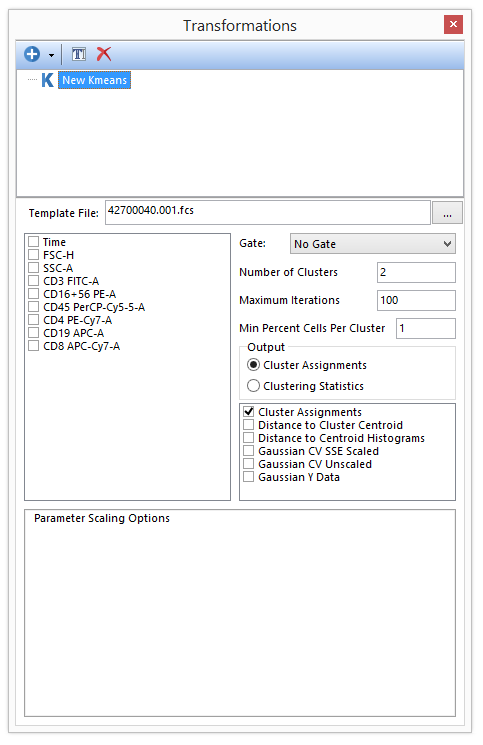
Figure 29.29 - A template file has been loaded into the New Kmeans dialog. 

 

5.通过选中参数名称旁边的框，选择参数以定义Kmeans聚类(图 29.24, Step 1)。
6.如果需要，请选择或更改每个所选参数的相应参数缩放选项(Parameter Scaling Options)(如下图第2步)。

 

Figure 29.30 - Choosing the parameters to perform k-means cluster analysis. 

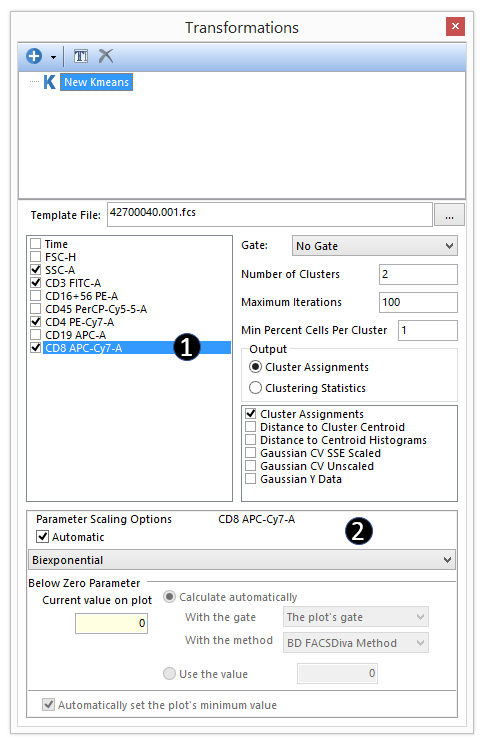
Figure 29.30 - Choosing the parameters to perform k-means cluster analysis. 

 

 

此时可以设置多个选项：

6.(选择的)从Gate 菜单中选择一个门如果您有兴趣仅对属于它的事件进行聚类。
7.设置该Number of Clusters这些事件应该被聚集。这相当于重心的数量。
8.设置Maximum Iterations(最多迭代次数)的数量此值表示FCS Express在退出聚集过程之前应执行的最大迭代次数。
9.设置Minimum Percent of Cells Per Cluster(每个聚集细胞数的最小百分比)该值表示聚集的最小大小(以百分比表示)。
10.设置Kmeans 聚集的输出类型。

 

可用的选择是Clustering Assignments(聚类分配)和Clustering Statistics(聚类统计)。请参阅下面的详细清单说明每个选项：

•Clustering Assignments(聚类分配)通过选择此输出样式，可以为群集执行的每个事件分配以下统计信息：
oCluster Assignment:指示群集成员的内部标签将自动分配给每个事件。该标签由FCS Express用于集群的热图表示，但也可以通过数据网格。
oDistance to Cluster Centroid:给定事件与其聚集的质心的距离。值作为唯一直方图绘制。
oDistance to centroid Histograms:与聚集中心距离相同，但在这种情况下，值分组，因此为每个聚集分别绘制。聚集的编号从1到Number of Clusters(聚集数)。
oGaussian CV SSE Scaled:在该表示中，每个事件根据其聚集成员进行绘制，因此集群显示为分离的直方图。由于聚集成员身份是从1到Number of Clusters(聚集数)的整数值，引入了人为噪音来分散数据。Gaussian SSE scaled意味着用于表示每个聚集的高斯(正态分布)的标准偏差与簇的平方误差之和成比例。
oGaussian CV Unscaled:在该表示中，每个事件根据其聚集成员进行绘制，因此集群显示为分离的直方图。由于聚集成员身份是从1到Number of Clusters(聚集数)的整数值，引入了人为噪音来分散数据。Gaussian CV Unscaled:意味着用于表示每个聚集的高斯(正态分布)的标准偏差在簇之间是相同的。
oGaussian Y Data:事件按照高斯(正态分布)绘制。

 

•Clustering Statistics(聚类统计)。通过选择此输出样式，可以通过绘图和数据网格访问以下统计信息数据网格：
oKmeans Cluster ID:一个整数值，从0到Clusters-1的数量。
oCentroid coordinates:给出了为聚集的考虑的每个参数的每个质心的坐标。
oSum Of Square (WCSS):针对每个聚集报告了群内平方和。

 

下表列出了适合显示每个输出样式的对象：

 

能被展示作为

Heatmap

1D 或 2D 点图

数据网格

Clustering Assignments(聚类分配)

Cluster Assignment:

Y

 

Y

聚集中心距离:

 

Y

Y

重心直方图的距离:

 

Y

Y

Gaussian CV SSE Scaled:

 

Y

Y

Gaussian CV Unscaled:

 

Y

Y

Gaussian Y Data:

 

Y

Y

Clustering Statistics(聚类统计)。

 

 

Y

Y

 

11.此k-means聚类现在已经被定义并自动计算。k-means 聚类 现在可以将它们于显示和分析的点图。(请参见Applying a k-means Cluster Analysis应用 k-means聚类分析)。

 

www.denovosoftware.com